先前我們利用廣度優先搜尋，找到圖中兩節點之間的最短路徑，其中所謂「最短」是指「經過最少的邊」。可是這樣的路徑卻未必是最快路徑，因為現實生活中不會每條路徑的距離或交通狀況都一樣。如果想要像一個聰明的導航系統，找出最快的路徑該怎麼做呢？

我們先想像在圖的邊上面加上數字，也就是所謂的權重(weight)，邊上有權重的圖叫做賦權圖或加權圖(weighted graph)。權重可以視為是經過一條邊所需的成本，在實際問題中它可以代表距離、時間、金錢等各種意義。

圖片來源：GeeksforGeeks

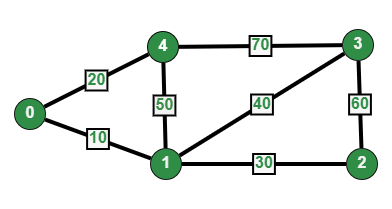
利用Dijkstra演算法，可以在賦權圖中找出成本最低，即權重總和最小的路徑，下述例子以距離最短表達，當然權重實際代表意義可能依問題改變。

Dijkstra演算法的方法是從起始節點開始，每次選擇距離最近的節點，並且逐步更新起點到各節點的最短距離。

以上方的圖來說，假設我們要從0到3，我們可以先把起始點到所有節點的距離暫時定為無窮遠，因為目前尚不知道到任何節點的距離。

首先檢查起點的鄰居，若無目標節點，將起點與鄰居的距離更新。

接著進行幾個步驟：

1. 選擇目前距離起點最近的節點n，計算起點經過節點n到所有節點n鄰居的距離，如果比紀錄中的當前距離短，就更新資料。
2. 計算完所有鄰居的距離，節點n就算是已訪問過，之後不必再檢查。
3. 重複上述步驟，直到目的地節點已被訪問，或者未訪問節點的距離都是無窮遠(沒有路徑存在)。

根據紀錄，我們選擇目前最近的節點1，起點經過節點1到鄰居4, 3, 2的距離分別是60, 50, 40，接著可以更新表格。其中到達4的距離為60，並沒有比原本的紀錄20短，所以不更新。最後將1標為已訪問。

接著選擇當前最近的節點4，重複上面的步驟，有較短路徑即更新表格。以4來說，經過4到達節點3的距離為90，不更新資料。

以此類推，最終直到目標節點3也被訪問後，如下表格中0到3的距離50即是到目的地的最短距離。

當然此處只是記錄了距離，如果想要知道中間的路徑，則可以每當更新最短距離的時候也記錄該節點的父節點，最後由終點回溯每一個節點的父節點直到起點，即為最短距離的路徑。例如更新節點1距離時記錄父節點為0，更新節點3距離時記錄父節點為1，最後從3回推最短路徑為0-1-3

Dijkstra演算法還有很多的變化型，也可以用在有向圖上，但基本上沒有辦法操作有權重為負值的圖(除非多次訪問節點，但這也就降低了執行效率)。要操作有負權重的圖可以參考Bellman–Ford演算法。

Dijkstra演算法的執行時間取決於操作時的資料結構，如果是使用陣列來儲存節點，執行時間為O(|V|²)，但如果改成使用堆積，執行時間可以縮短為O(|E|+|V| log |V|)。